LSTM and GRU
Table of Contents
LSTM #
The avoid the problem of vanishing gradient and exploding gradient in vanilla RNN, LSTM was published, which can remember information for longer periods of time.
Here is the structure of LSTM:
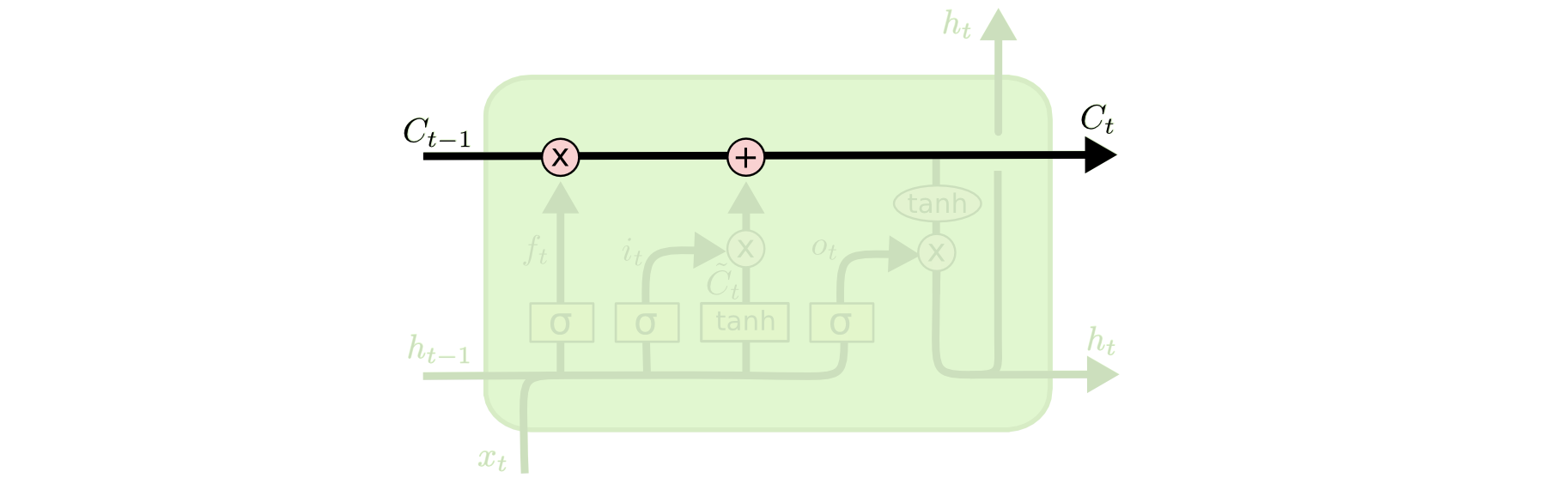
The calculate procedure are:
\[\begin{aligned} f_t&=\sigma(W_f\cdot[h_{t-1},x_t]+b_f)\\ i_t&=\sigma(W_i\cdot[h_{t-1},x_t]+b_i)\\ o_t&=\sigma(W_o\cdot[h_{t-1},x_t]+b_o)\\ \tilde{C_t}&=tanh(W_C\cdot[h_{t-1},x_t]+b_C)\\ C_t&=f_t\ast C_{t-1}+i_t\ast \tilde{C_t}\\ h_t&=o_t \ast tanh(C_t) \end{aligned}\]
\(f_t\),\(i_t\),\(o_t\) are forget gate, input gate and output gate respectively. \(\tilde{C_t}\) is the new memory content. \(C_t\) is cell state. \(h_t\) is the output.
Use \(f_t\) and \(i_t\) to update \(C_t\), use \(o_t\) to decide which part of hidden state should be outputted.
GRU #
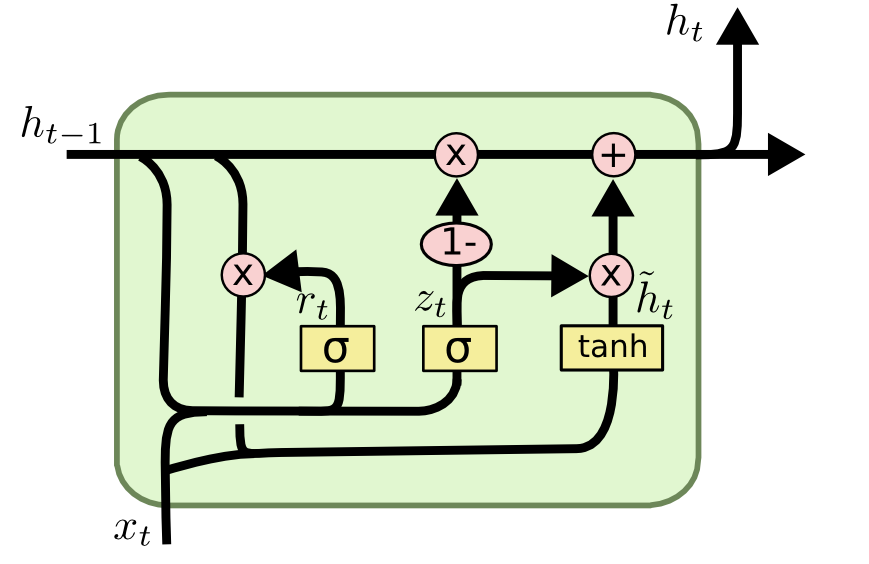
\[\begin{aligned} z_t&=\sigma(W_z\cdot[h_{t-1},x_t])\\ r_t&=\sigma(W_r\cdot[h_{t-1},x_t])\\ \tilde{h_t}&=tanh(W\cdot[r_t \ast h_{t-1},x_t])\\ h_t&=(1-z_t)\ast h_{t-1}+z_t \ast \tilde{h_t} \end{aligned}\]
\(z_t\) is update gate, \(r_t\) is reset gate, \(\tilde{h_t}\) is candidate activation, \(h_t\) is activation.
Compare with LSTM, GRU merge cell state and hidden state to one hidden state, and use \(z_t\) to decide how to update the state rather than \(f_t\) and \(i_t\).