Models and Architectures in Word2vec

Table of Contents

Generally, word2vec is a language model to predict the words probability based on the context. When build the model, it create word embedding for each word, and word embedding is widely used in many NLP tasks.

Models #

CBOW (Continuous Bag of Words) #

Use the context to predict the probability of current word. (In the picture, the word is encoded with one-hot encoding, \(W_{V*N}\) is word embedding, and \(W_{V*N}^{’}\), the output weight matrix in hidden layer, is same as \(\hat{\upsilon}\) in following equations)

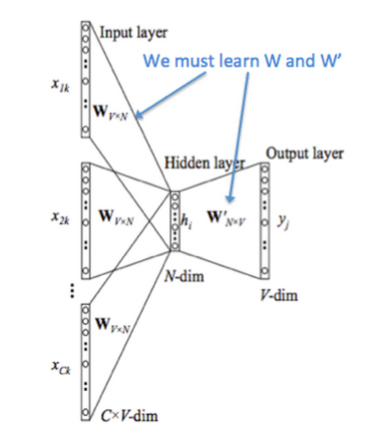
Context words’ vectors are \(\upsilon_{c-n} … \upsilon_{c+m}\) (\(m\) is the window size)
Context vector \(\hat{\upsilon}=\frac{\upsilon_{c-m}+\upsilon_{c-m+1}+…+\upsilon_{c+m}}{2m}\)
Score vector \(z_i = u_i\hat{\upsilon}\), where \(u_i\) is the output vector representation of word \(\omega_i\)
Turn scores into probabilities \(\hat{y}=softmax(z)\)
We desire probabilities \(\hat{y}\) match the true probabilities \(y\).

We use cross entropy \(H(\hat{y},y)\) to measure the distance between these two distributions. \[H(\hat{y},y)=-\sum_{j=1}^{\lvert V \rvert}{y_j\log(\hat{y}_j)}\]

\(y\) and \(\hat{y}\) is accurate, so the loss simplifies to: \[H(\hat{y},y)=-y_j\log(\hat{y})\]

For perfect prediction, \(H(\hat{y},y)=-1\log(1)=0\)

According to this, we can create this loss function:

\[\begin{aligned} minimize\ J &=-\log P(\omega_c\lvert \omega_{c-m},…,\omega_{c-1},…,\omega_{c+m}) \\ &= -\log P(u_c \lvert \hat{\upsilon}) \\ &= -\log \frac{\exp(u_c^T\hat{\upsilon})}{\sum_{j=1}^{\lvert V \rvert}\exp (u_j^T\hat{\upsilon})} \\ &= -u_c^T\hat{\upsilon}+\log \sum_{j=1}^{\lvert V \rvert}\exp (u_j^T\hat{\upsilon}) \end{aligned}\]

Skip-Gram #

Use current word to predict its context.

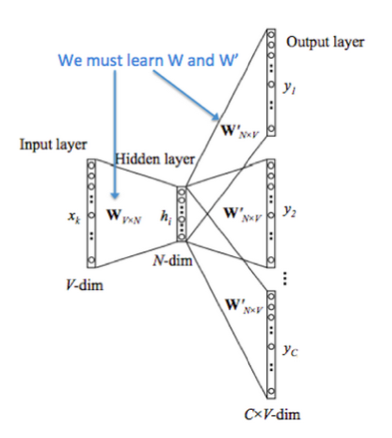
We get the input word’s vector \(\upsilon_c\)
Generate \(2m\) score vectors, \(u_{c-m},…,u_{c-1},…,u_{c+m}\).
Turn scores into probabilities \(\hat{y}=softmax(u)\)
We desire probabilities \(\hat{y}\) match the true probabilities \(y\).

\[\begin{aligned} minimize J &=-\log P(\omega_{c-m},…,\omega_{c-1},\omega_{c+1},…\omega_{c+m}\lvert \omega_c)\\ &=-\log \prod_{j=0,j\ne m}^{2m}P(\omega_{c-m+j}\lvert \omega_c)\\ &=-\log \prod_{j=0,j\ne m}^{2m}P(u_{c-m+j}\lvert \upsilon_c)\\ &=-\log \prod_{j=0,j\ne m}^{2m}\frac{\exp (u^T_{c-m+j}\upsilon_c)}{\sum_{k=1}^{\lvert V \rvert}{\exp (u^T_k \upsilon_c)}}\\ &=-\sum_{j=0,j\ne m}^{2m}{u^T_{c-m+j}\upsilon_c+2m\log \sum_{k=1}^{\lvert V \rvert} \exp(u^T_k \upsilon_c)} \end{aligned}\]

Architectures #

Minimize \(J\) is expensive, you need to calculate the probability of each word in vocabulary list. There are two ways to reduce the computation. Hierarchical Softmax and Negative Sampling.

Hierarchical Softmax #

Encode words into a huffman tree, then each word has a Huffman code. The probability of it’s probability \(P(w\lvert Context(\omega))\) can change to choose the path from root to the leaf node, each node is a binary classification. Suppose code \(0\) is a positive label, \(1\) is negative label. If the probability of a positive classification is \[\sigma(X^T_\omega \theta)=\frac{1}{1+e^{-X^T_\omega}}\]

Then the probability of negative classification is \[1-\sigma(X^T_\omega \theta)\]

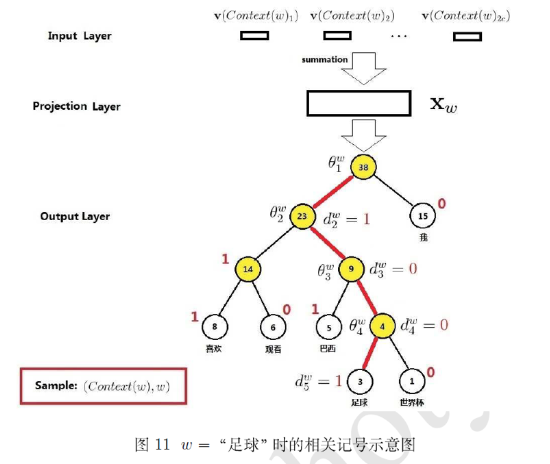`足球`'s Huffman code is \\(1001\\), then it's probability in each node are

\[\begin{aligned} p(d_2^\omega\lvert X_\omega,\theta^\omega_1&=1-\sigma(X^T_\omega \theta^\omega_1))\\ p(d^\omega_3\lvert X_\omega,\theta^\omega_2&=\sigma(X^T_\omega \theta^\omega_2))\\ p(d^\omega_4\lvert X_\omega,\theta^\omega_3&=\sigma(X^T_\omega \theta^\omega_3))\\ p(d^\omega_5\lvert X_\omega,\theta^\omega_4&=1-\sigma(X^T_\omega \theta^\omega_4))\\ \end{aligned}\]

where \(\theta\) is parameter in the node.

The probability of the 足球 is the production of these equation.

Generally,

\[p(\omega\lvert Context(\omega))=\prod_{j=2}^{l\omega}p(d^\omega_j\lvert X_\omega,\theta^\omega_{j-1})\]

This reduce the calculation complexity to \(log(n)\) instead of \(n\)

Negative Sampling #

This method will choose some negative sample, then add the probability of the negative word into loss function. The optimisation target becomes maximise the positive words’ probability and minimise the negative words’ probability.

Let \(P(D=0 \lvert \omega,c)\) be the probability that \((\omega,c)\) did not come from the corpus data. Then the objective function will be

\[\theta = \text{argmax} \prod_{(\omega,c)\in D} P(D=1\lvert \omega,c,\theta) \prod_{(\omega,c)\in \tilde{D}} P(D=0\lvert \omega,c,\theta)\]

where \(\theta\) is the parameters of the model(\(\upsilon\) and \(u\)).

update 04-04-20

I found this two articles pretty useful: Language Models, Word2Vec, and Efficient Softmax Approximations and Word2vec from Scratch with NumPy.