Near-duplicate with SimHash
Table of Contents
Before talking about SimHash, let’s review some other methods which can also identify duplication.
Longest Common Subsequence(LCS) #
This is the algorithm used by diff command. It is also edit distance with insertion and deletion as the only two edit operations.
This works good for short strings. However, the algorithm’s time complexity is \(O(m*n)\), if two strings’ lengths are \(m\) and \(n\) respectively. So it’s not suitable for large corpus. Also, if two corpus consists of same paragraph but the order is not same. LCS treat them as different corpus, and that’s not we expected.
Bag of Words(BoW) #
Transform document into the words it contains, then using Jaccard Similarity to calculate the similarity.
For example, if document A contains {a,b,c} and B contains {a,b,d}, then \[Similarity = \frac{A \cap B}{A \cap B} = \frac{\{a,b\}}{\{a,b,c,d\}}=\frac{1}{2}\]
Shingling (n-gram) #
BoW drops the word context information. In order to take word context into consideration, we convert sentences into phrases. For instance, roses are red and violets are blue will convert to roses are red, are red and, red and voilets …
Hashing #
Saving shingling result take k times disk space if using k words phrase. To solve this problem, save phrase’s hashing value instead of string.
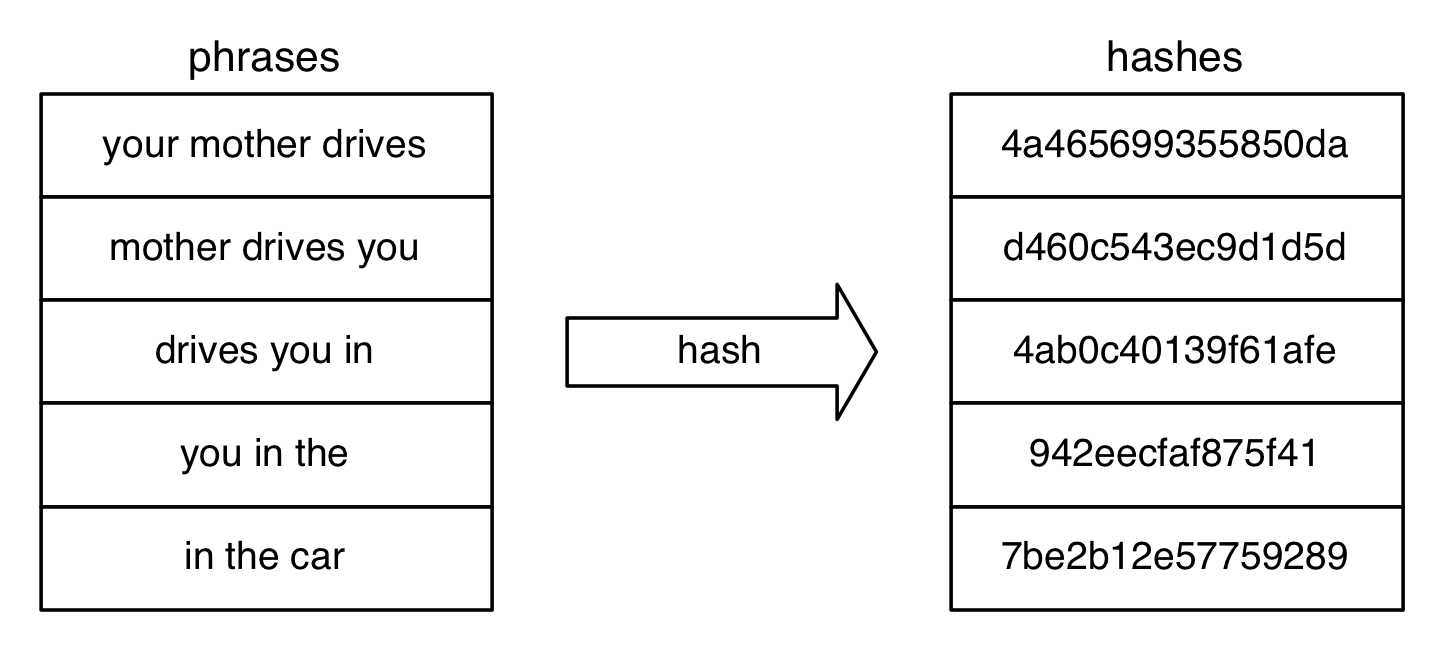
MinHash #
The larger the document is, the more the hashing needs to compare. Is there a way to map documents to constant value? MinHash tackles this problem.
It uses \(k\) hashing functions to calculate the phrase hashes. Then for each hashing function, using the minimal hashing result as signature. Finally, we get \(k\) hashing value as document’s signature. The procedure is shown below.


Compare with Hashing, MinHash successfully reduce the time complexity and storage complexity to \(O(1)\), an improvement over \(O(m+n)\) and \(O(n)\), where n is the phrase number, m is the phrase number to compare.
SimHash #
For a given document, how to find it’s most similar document? If using MinHash, we need to travel the whole corpus. Is there any more effective method? SimHash comes to the rescue.
For a set of input hashes, SimHash will generate a fingerprint(f-bits vector) for the input And the produced hashes has a property: similar input hashes generate similar fingerprint. So the dissimilarity of two documents can be calculated by the XOR of two fingerprint. In google’s Detecting Near-Duplicates for Web Crawling paper, they map 8B web-pages to 64 bits. If two bits differ less than 3 bits, then two web-pages are similar.
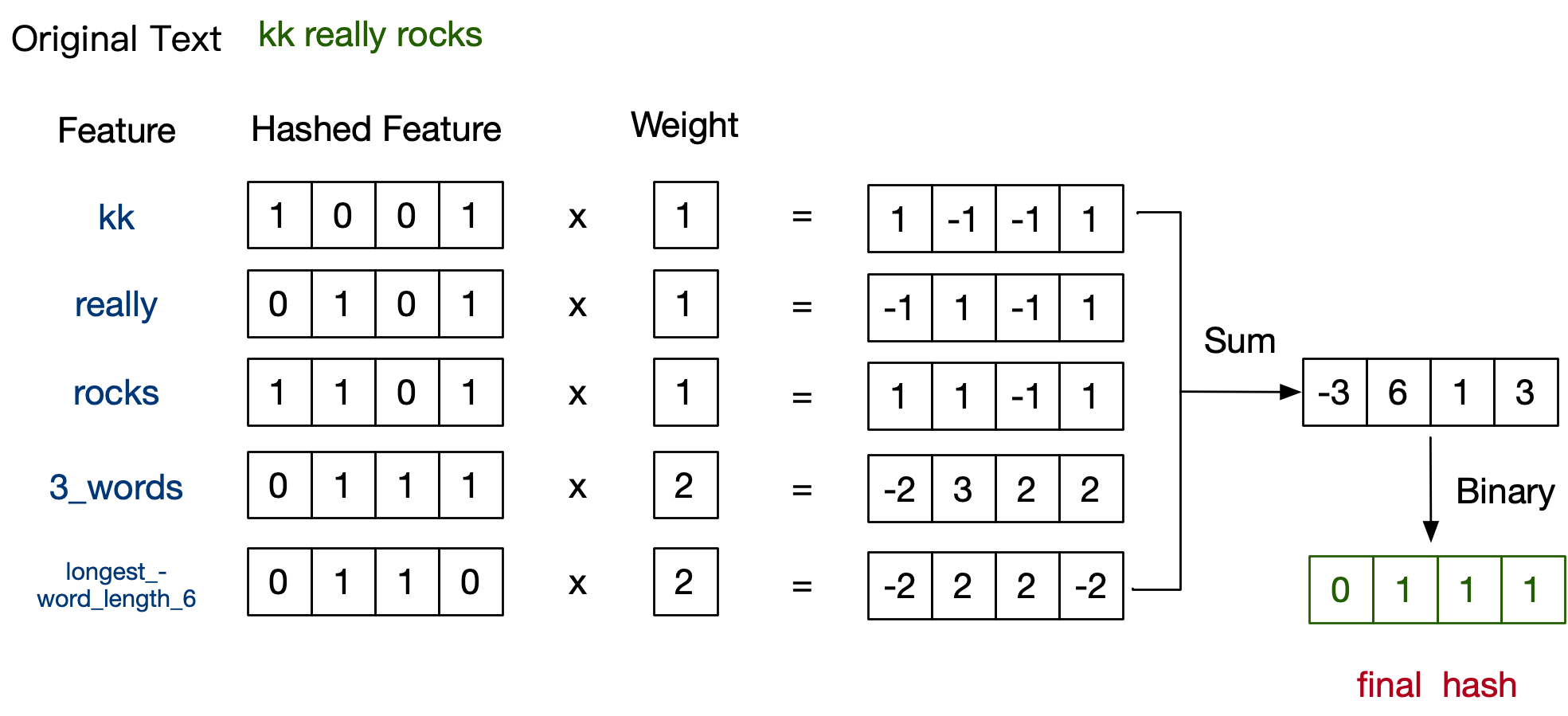
The calculation of SimHash is quiet simple. Given a set of features extracted from the document and their weights, we’ll maintain f-bits vector \(V\), and initialize it to zero. Each feature will also hash to f-bit value \(V_i\). Then each dimension of \(V_i\) will multiply by it’s weight \(W_i\) and add this new value to \(V\). If i-th bits if 1, then \(V\) is incremented by the weight of that feature. Otherwise \(V\) is decremented by the weight. When all features have been processed, \(V\) contains positive and negative dimension. Mapping positive values to 1 and negative numbers to 0 to get the final hash value.
\[V = zero\_or\_one(\sum{W_i*inc\_or\_dec(V_i)})\]
How to generate features from document #
One easy way to do this is to use a window to get sub-string from document. For each sub-string, using the hash value of string as features, and the count of this string as weight.
For example, if we has this sentence: kk really rocks!.
First, pre-processing this sentence to kkreallyrocks.
Then using a window of 4 to generate sub-string from the sentence. We’ll get the sub-string and their count: (kkre, 1), (krea, 1), (real, 1) etc.
Suppose we only get these first 3 sub-string and their hash values are 1001, 0101 and 1101 respectively. Then the final \(V\) should be 1101
How to find similar document #
Iterating over all document and compare with target simhash value is a time consuming operation. Is there any smart way to accomplish this task? In Google’s paper, they published a very neat algorithm.
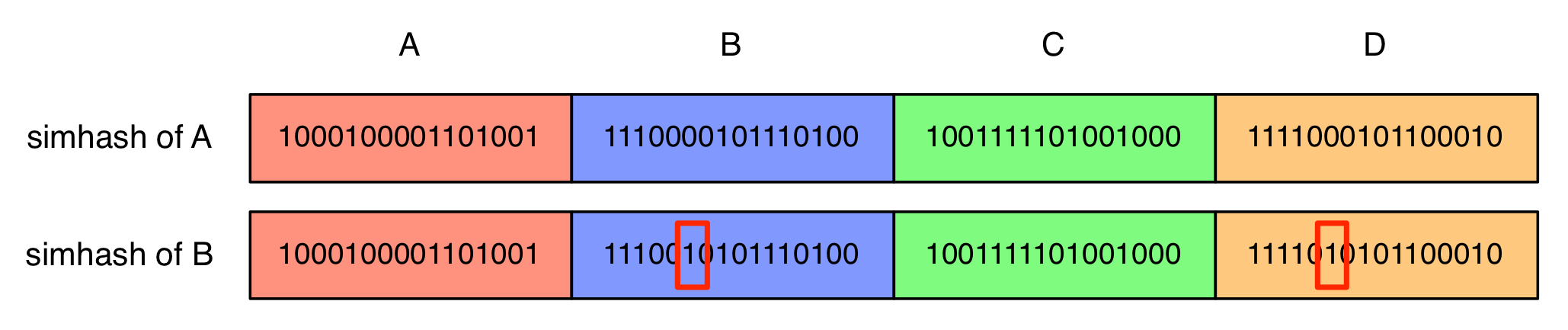
If the hash value is a 64-bit vector, and we want to find the document which is 2-bit differs with the target. Then we can divided the vector to 4 part: \(A\), \(B\), \(C\) and \(D\). Then we know that at least two part should be the identical.
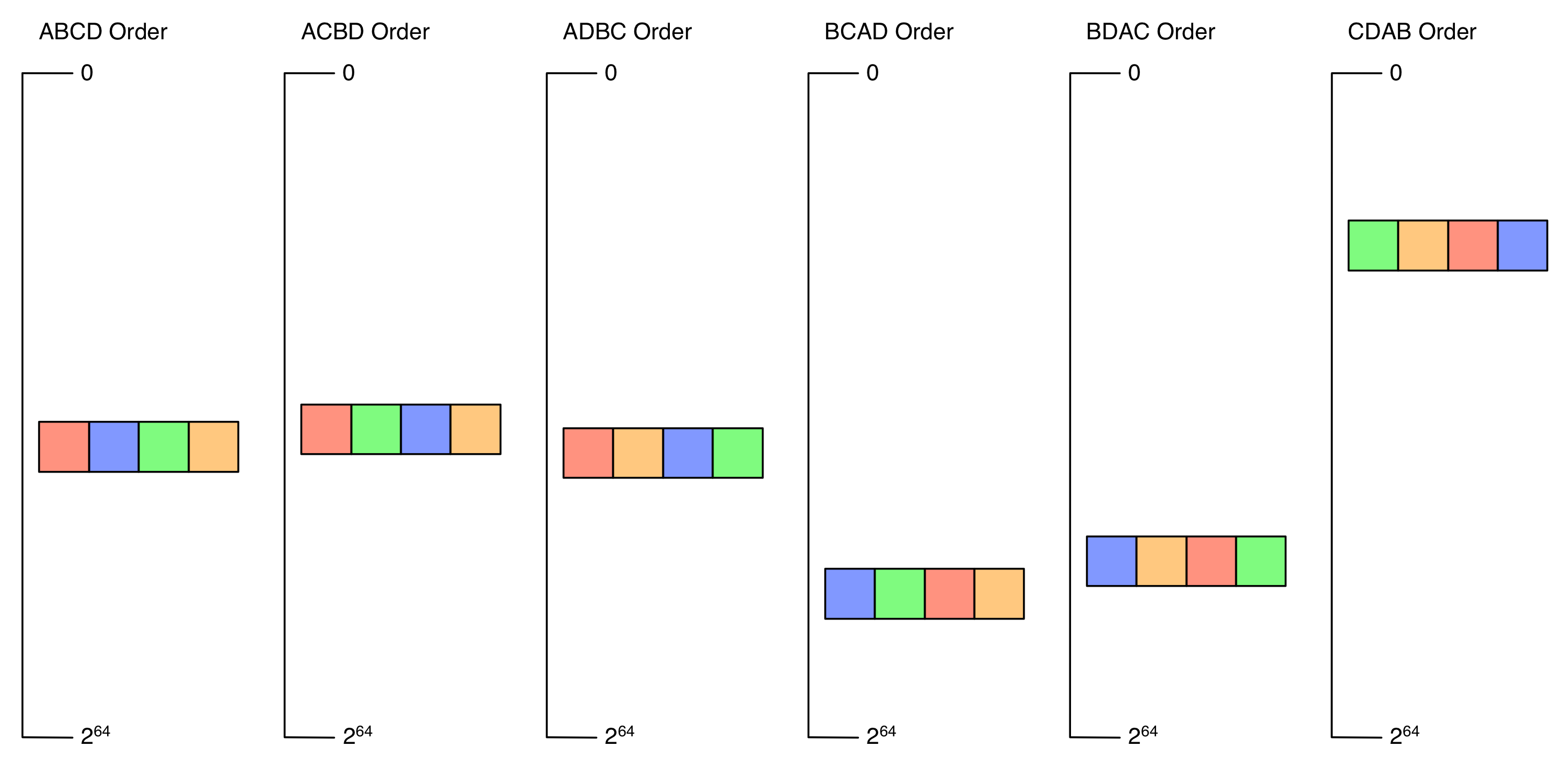
Suppose part \(A\) and \(B\) is identical, if we have sorted the hash by \(ABCD\) order, we can easily find all hash that \(AB\) part is identical. Then we can compare the rest part \(B\) and \(C\) and find hash vectors that differs from target at most 2 bit. If you have 8B(\(2^{34}\)) document and documents are distributed uniformly at random, on average, you only need to compare \(2^{34-32}=4\) fingerprints.
Besides \(AB\), \(AC\), \(AD\), \(BC\), \(BD\) and \(CD\) may also be identical. So you need to keep \(C_4^2=6\) sorted list, and compare 4 fingerprints in each list. You don’t need to compare 8B documents anymore, that’s a great improvement.
Depending on the fingerprints’ bit and documents number, you need to find a optimal number to split the hash value.