Parameters in doc2vec
Table of Contents
Here are some parameter in gensim’s doc2vec class.
window #
window is the maximum distance between the predicted word and context words used for prediction within a document. It will look behind and ahead.
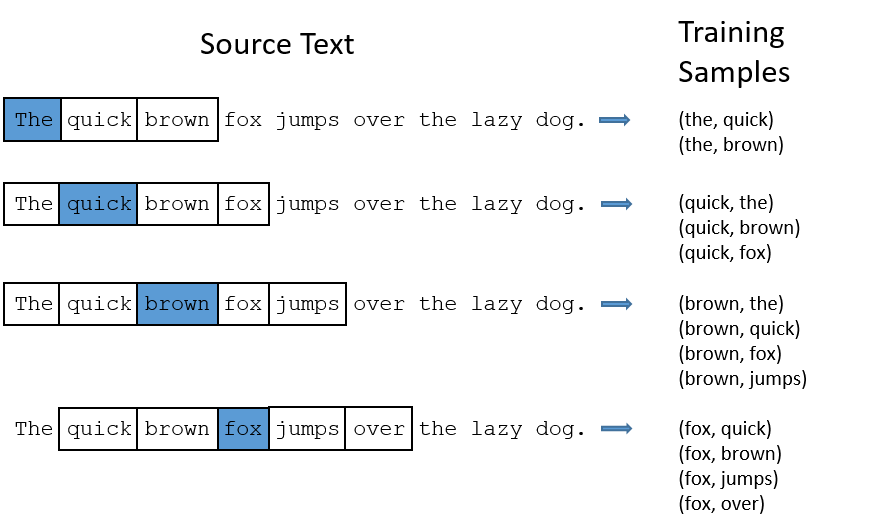
In skip-gram model, if the window size is 2, the training samples will be this:(the blue word is the input word)
min_count #
If the word appears less than this value, it will be skipped
sample #
High frequency word like the is useless for training. sample is a threshold for deleting these higher-frequency words. The probability of keeping the word \(w_i\) is:
\[P(w_i) = (\sqrt{\frac{z(\omega_i)}{s}} + 1) \cdot \frac{s}{z(\omega_i)}\]
where \(z(w_i)\) is the frequency of the word and \(s\) is the sample rate.
This is the plot when sample is 1e-3.

negative #
Usually, when training a neural network, for each training sample, all of the weights in the neural network need to be tweaked. For example, if the word pair is (‘fox’, ‘quick’), then only the word quick’s neurons should output 1, and all of the other word neurons should output 0.
But it would takes a lot of time to do this when we have billions of training samples. So, instead of update all of the weight, we random choose a small number of “negative” words (default value is 5) to update the weight.(Update their wight to output 0).
So when dealing with word pair (‘fox’,‘quick’), we update quick’s weight to output 1, and other 5 random words’ weight to output 1.
The probability of selecting word \(\omega_i\) is \(P(\omega_i)\):
\[P(\omega_i)=\frac{{f(\omega_i)}^{{3}/{4}}}{\sum_{j=0}^{n}\left({f(\omega_j)}^{{3}/{4}}\right)}\]
\(f(\omega_j)\) is the frequency of word \(\omega_j\).