The Annotated The Annotated Transformer

Table of Contents

Thanks for the articles I list at the end of this post, I understand how transformers works. These posts are comprehensive, but there are some points that confused me.

First, this is the graph that was referenced by almost all of the post related to Transformer.

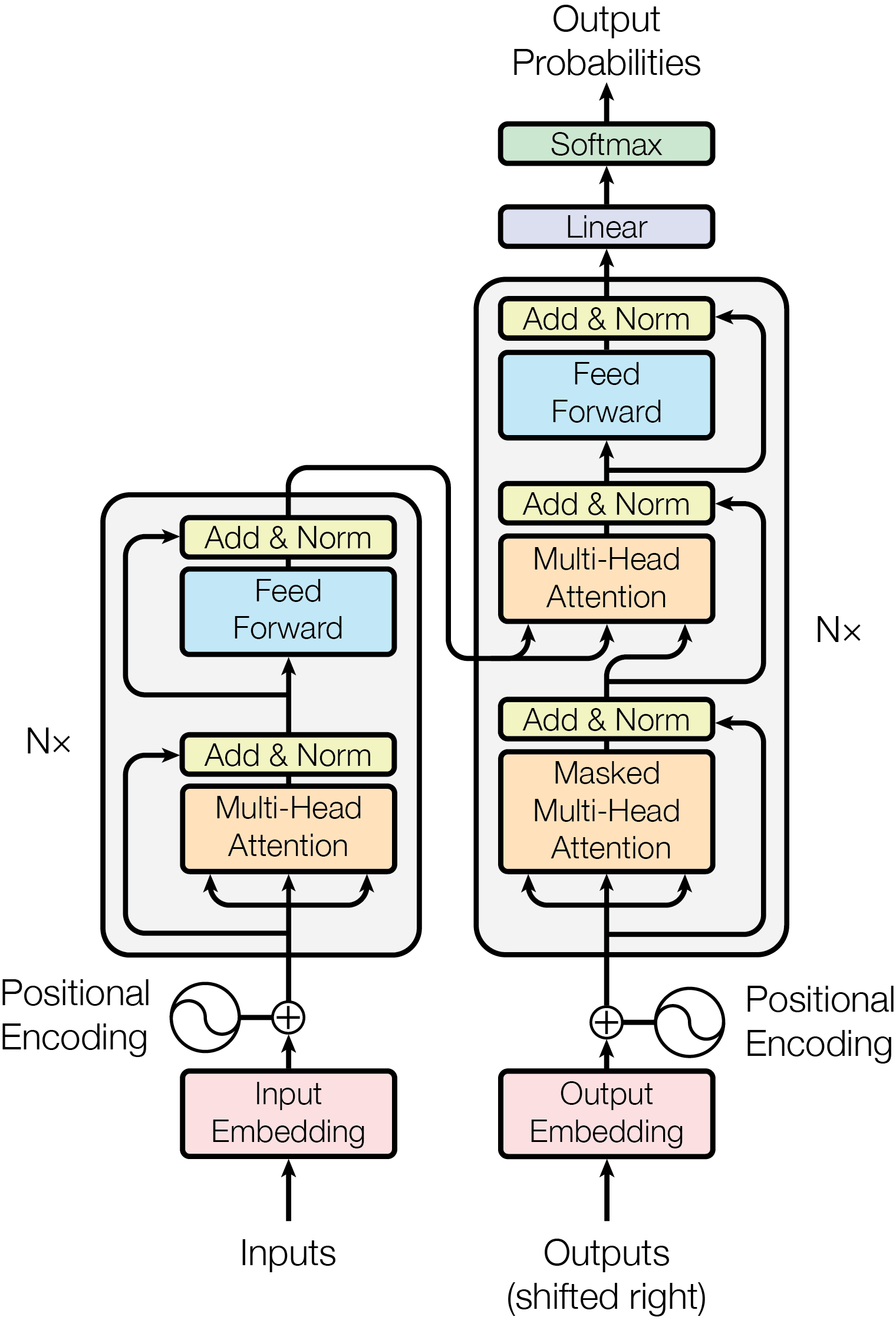
Transformer consists of these parts: Input, Encoder*N, Output Input, Decoder*N, Output. I’ll explain them step by step.

Input #

The input word will map to 512 dimension vector. Then generate Positional Encoding(PE) and add it to the original embeddings.

Positional Encoding #

The transformer model does not contains recurrence and convolution. In order to let the model capture the sequence of input word, it add PE into embeddings.

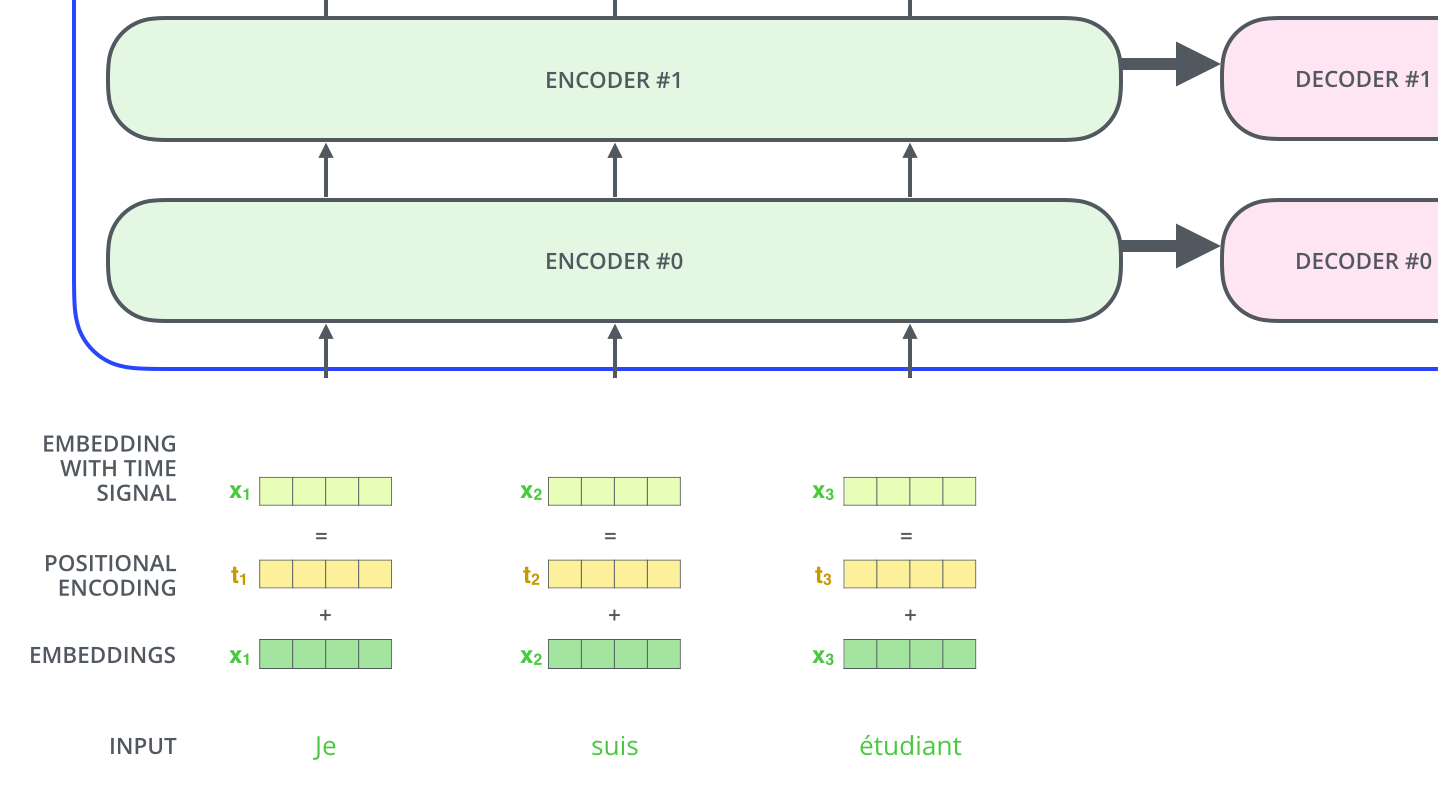
PE will generate a 512 dimension vector for each position:

\[\begin{align*} PE_{(pos,2i)} = sin(pos / 10000^{2i/d_{model}}) \\ PE_{(pos,2i+1)} = cos(pos / 10000^{2i/d_{model}}) \end{align*}\] The even and odd dimension use sin and cos function respectively.

For example, the second word’s PE should be: \(sin(2 / 10000^{0 / 512}), cos(2 / 10000^{0 / 512}), sin(2 / 10000^{2 / 512}), cos(2 / 10000^{2 / 512})\text{…}\)

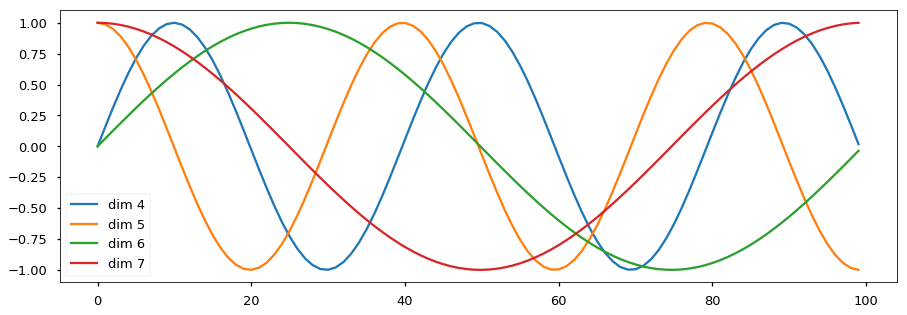
The value range of PE is (-1,1), and each position’s PE is slight different, as cos and sin has different frequency. Also, for any fixed offset k, \(PE_{pos+k}\) can be represented as a linear function of \(PE_{pos}\).

For even dimension, let \(10000^{2i/d_{model}}\) be \(\alpha\), for even dimension:

\[\begin{aligned} PE_{pos+k}&=sin((pos+k)/\alpha) \\ &=sin(pos/\alpha)cos(k/\alpha)+cos(pos/\alpha)sin(k/\alpha)\\ &=PE_{pos\_even}K_1+PE_{pos\_odd}K_2 \end{aligned}\]

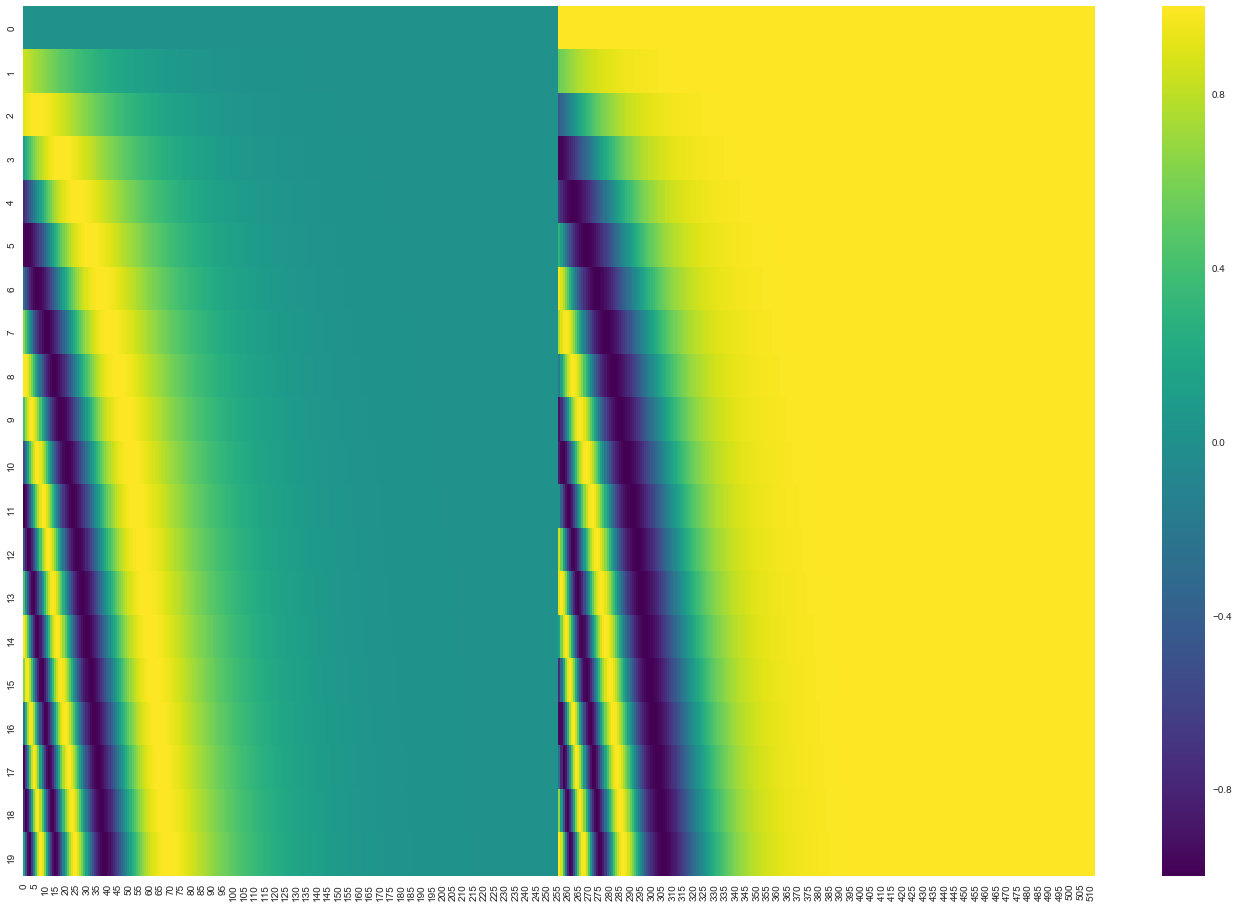
The PE implementation in tensor2tensor use sin in first half of dimension and cos in the rest part of dimension.

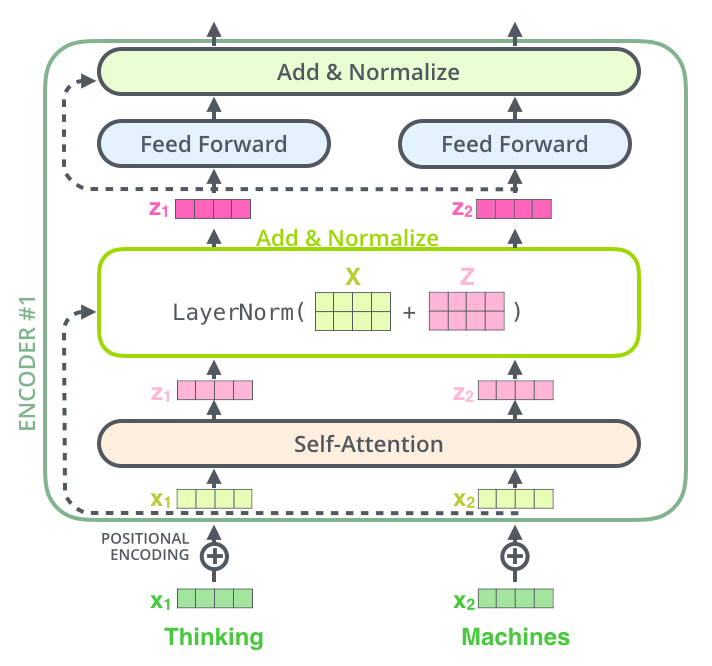
Encoder #

There are 6 Encoder layer in Transformer, each layer consists of two sub-layer: Multi-Head Attention and Feed Forward Neural Network.

Multi-Head Attention #

Let’s begin with single head attention. In short, it maps word embeddings to q k v and use q k v vector to calculate the attention.

The input words map to q k v by multiply the Query, Keys Values matrix. Then for the given Query, the attention for each word in sentence will be calculated by this formula: \(\mathrm{attention}=\mathrm{softmax}(\frac{qk^T}{\sqrt{d_k}})v\), where q k v is a 64 dimension vector.

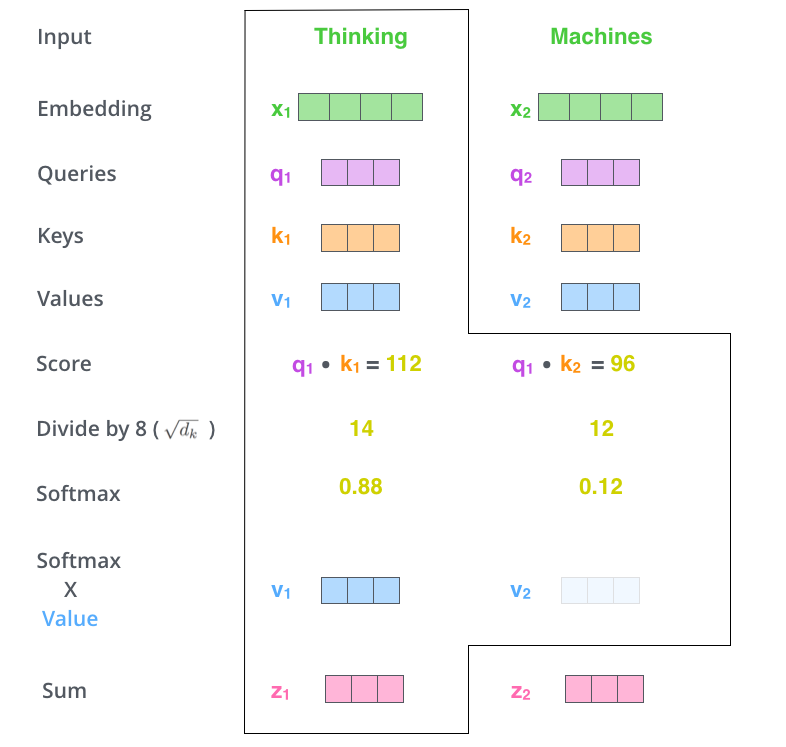
Matrix view:

\(Attention(Q, K, V) = \mathrm{softmax}(\frac{(XW^Q)(XW^K)^T}{\sqrt{d_k}})(XW^V)\) where \(X\) is the input embedding.

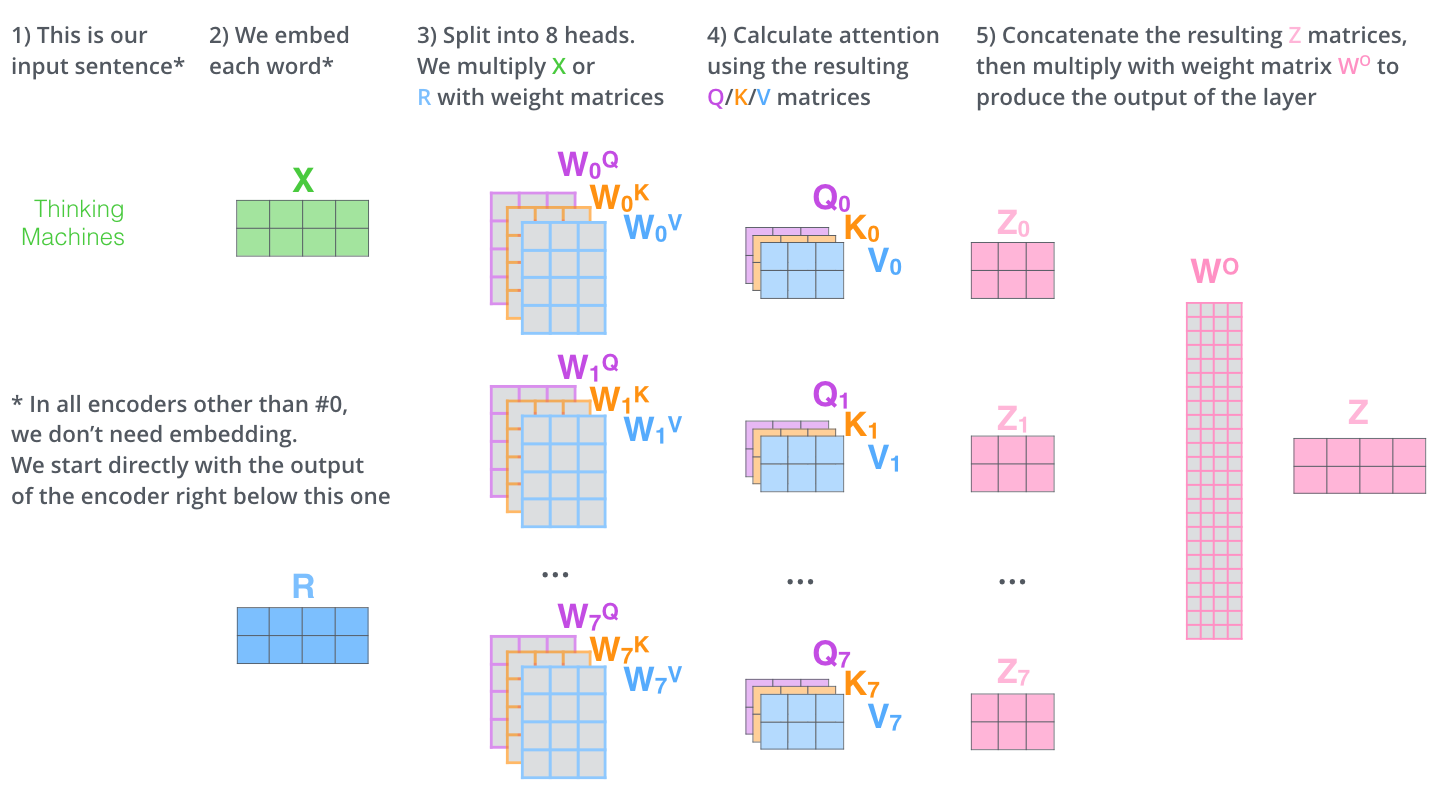
The single head attention only output a 64 dimension vector, but the input dimension is 512. How to transform back to 512? That’s why transformer has multi-head attention.

Each head has its own \(W^Q\) \(W^K\) \(W^V\) matrix, and produces \(Z_0,Z_1…Z_7\),(\(Z_0\)’s shape is (512, 64)) the concat the outputted vectors as \(O\). \(O\) will multiply a weight matrix \(W^O\) (\(W^O\)’s shape is (512, 512)) and the result is \(Z\), which will be sent to Feed Forward Network.

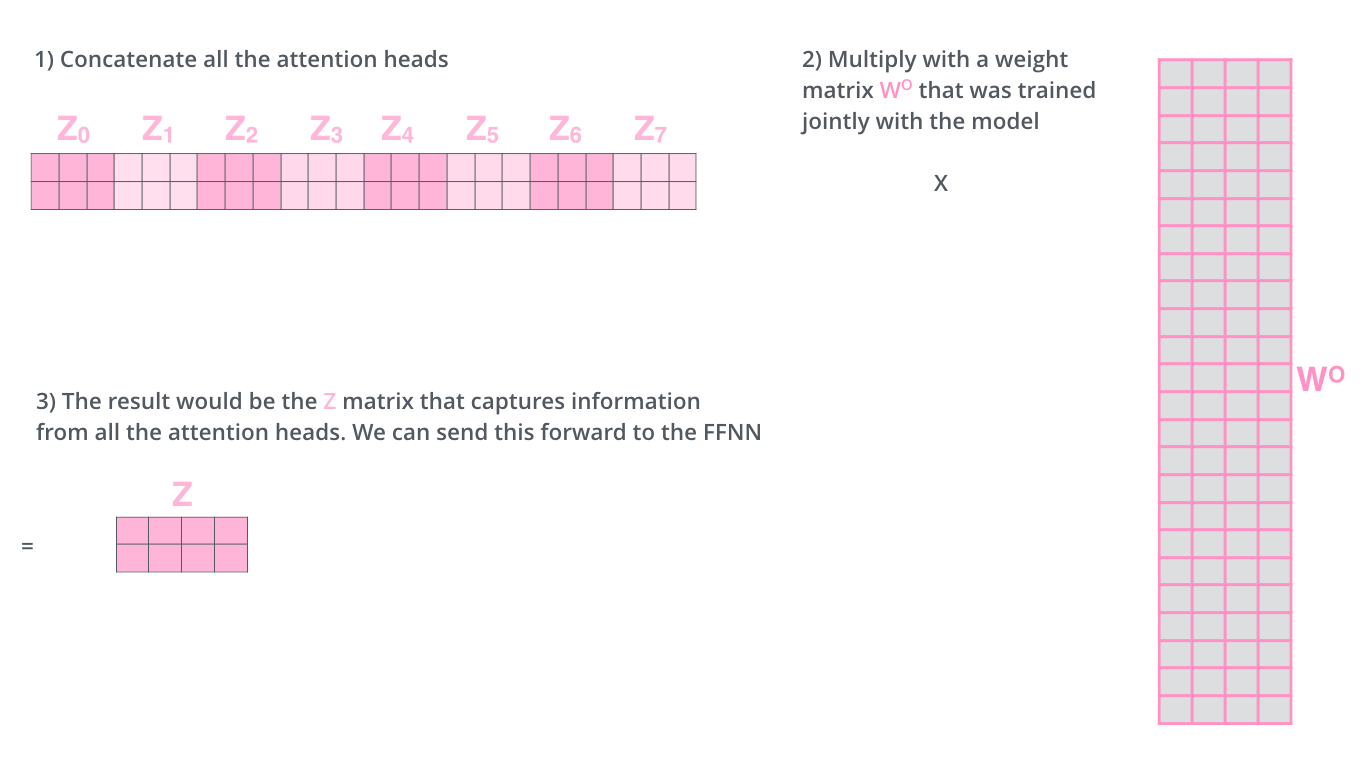
Multi-head attention allows the model to jointly attend to information from different representation subspaces at different positions.

The whole procedure looks like this:

Add & Norm #

This layer works like this line of code: norm(x+dropout(sublayer(x))) or x+dropout(sublayer(norm(x))). The sublayer is Multi-Head Attention or FF Network.

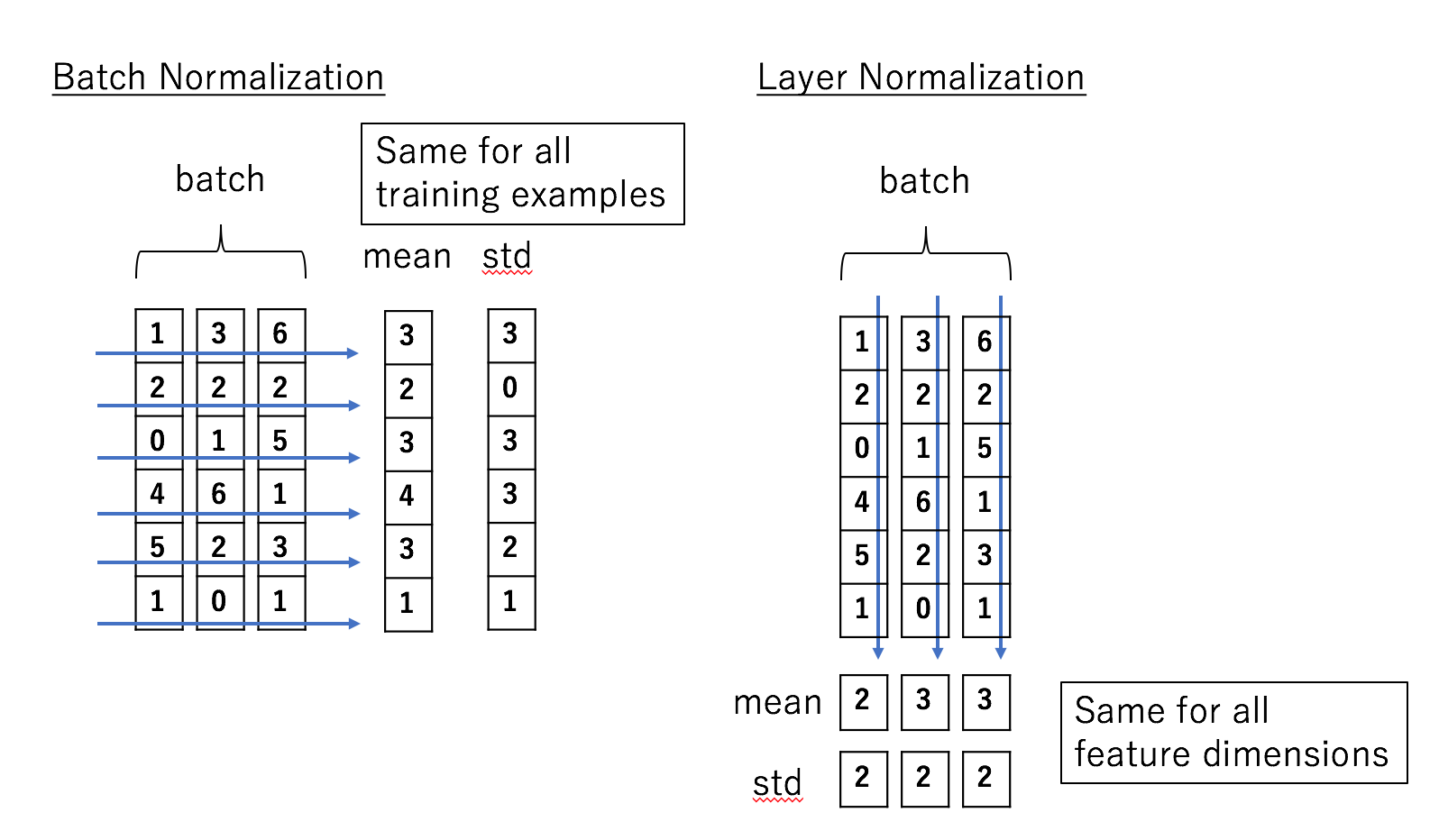
Layer Normalization #

Layer Norm is similar to Batch Normalization, but it tries to normalize the whole layer’s features rather than each feature.(Scale and Shift also apply for each feature) More details can be found in this paper.

Position-wise Feed Forward Network #

This layer is a Neural Network whose size is (512, 2048, 512). The exact same feed-forward network is independently applied to each position.

Output Input #

Same as Input.

Decoder #

The decoder is pretty similar to Encoder. It also has 6 layers, but has 3 sublayers in each Decoder. It add a masked multi-head-attention at the beginning of Decoder.

Masked Multi-Head Attention #

This layer is used to block future words during training. For example, if the output is <bos> hello world <eos>. First, we should use <bos> as input to predict hello, hello world <eos> will be masked to 0.

Key and Value in Decoder Multi-Head Attention Layer #

In Encoder, the q k v vector is generated by \(XW^Q\), \(XW^K\) and \(XW^V\). In the second sub-layer of Decoder, q k v was generated by \(XW^Q\), \(YW^K\) and \(YW^V\), where \(Y\) is the Encoder’s output, \(X\) is the <init of sentence> or previous output.

The animation below illustrates how to apply the Transformer to machine translation.

Output #

Using a linear layer to predict the output.